pandasのresampleとasfreqを使って、msオーダの時系列データをリサンプリングする

仕事でセンサデータをよく扱うのですが、リサンプリングするたびにその方法を調べていました。
最近やっとわかってきたので、今回は備忘録としてまとめます🐜

開発環境
サンプルプログラム
解説
考察
おわりに
参考文献

開発環境

開発環境は以下の通りです。Python＋pandasでの開発を想定しています。OSはWindowsでなくても大丈夫です。

項目	内容
OS	Windows 10
Python	3.6.8
numpy	1.18.1
pandas	1.0.1
matplotlib	3.1.3

サンプルプログラム

作成したサンプルプログラムは以下の通りです。環境さえあれば、コピペで動きます。

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
""" resampling

pandasを使って、msオーダでリサンプリングする

"""
__author__  = 'ari23(Twitter: @ari23ant)'
__version__ = '0.0.1'
__date__    = '2021/02/10'
__status__  = 'Development'

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


class TestResample:

    def __init__(self):
        self.msg = 'pandas resampling'

        # 時間
        self.fs = 50  # サンプリング周波数[Hz]
        self.timespan = 3  # 時間幅[s]

        # sin波
        self.sin_A = 2  # 振幅[]
        self.sin_f = 1  # 周期[Hz]

    def run(self):
        print(self.msg)

        # sin波作成
        t = np.arange(0, self.timespan, 1/self.fs)
        sin = self.sin_A * np.sin(2.0 * np.pi * self.sin_f * t)

        # s→msに変換
        t = t * 1000

        # sin波をプロット
        fig = plt.figure()
        ax = fig.add_subplot()
        ax.plot(t, sin, marker='.', lw=0, ms=3)
        ax.set_xlabel('time [ms]')
        ax.grid(b=True)

        # DataFrameに格納
        self.df1 = pd.DataFrame({'ts':t, 'sig':sin})
        #print(self.df1)

        # いったん日付に変換
        self.df1['ts'] = pd.to_datetime(self.df1['ts'], unit='ms')  # デフォルトはnsなのでmsに指定
        #print(self.df1)

        # indexにセット
        self.df1 = self.df1.set_index('ts')

        # 20ms→1ms
        self.df2 = self.df1.resample('1ms').interpolate()  # 線形補間
        #self.df2 = self.df1.resample('1ms').ffill()  # 前の値で補完

        # 20ms→1ms→5ms
        self.df3 = self.df2.asfreq('5ms')
        #self.df3 = self.df1.resample('5ms').interpolate()  # 20ms→5ms線形補間もできる

        # index解除
        self.df1.reset_index(inplace=True)
        self.df2.reset_index(inplace=True)
        self.df3.reset_index(inplace=True)

        # datetime64型→int64型｜msに戻す
        self.df1['ts'] = self.df1['ts'].astype('int64') / 10**6  # 最後の除算でns→msにする
        self.df2['ts'] = self.df2['ts'].astype('int64') / 10**6  # 最後の除算でns→msにする
        self.df3['ts'] = self.df3['ts'].astype('int64') / 10**6  # 最後の除算でns→msにする

        # 20ms→1msの結果をプロット
        fig = plt.figure()
        ax = fig.add_subplot()
        ax.plot(self.df2['ts'], self.df2['sig'], marker='.', lw=0, ms=3)
        ax.set_xlabel('time [ms]')
        ax.grid(b=True)

        # 20ms→1ms→5msの結果をプロット
        fig = plt.figure()
        ax = fig.add_subplot()
        ax.plot(self.df3['ts'], self.df3['sig'], marker='.', lw=0, ms=3)
        ax.set_xlabel('time [ms]')
        ax.grid(b=True)

        # プロット
        plt.show()

# 実行
proc = TestResample()
proc.run()

こちらを実行すると、3枚のグラフが出力されます。

解説

サンプルプログラムを解説します。

問題設定

今回は以下の設定で、sin波を取得したとします。

項目	設定値
サンプリング周波数[Hz]	50
データ取得時間[s]	3
sin波振幅[]	2
sin波周期[Hz]	1

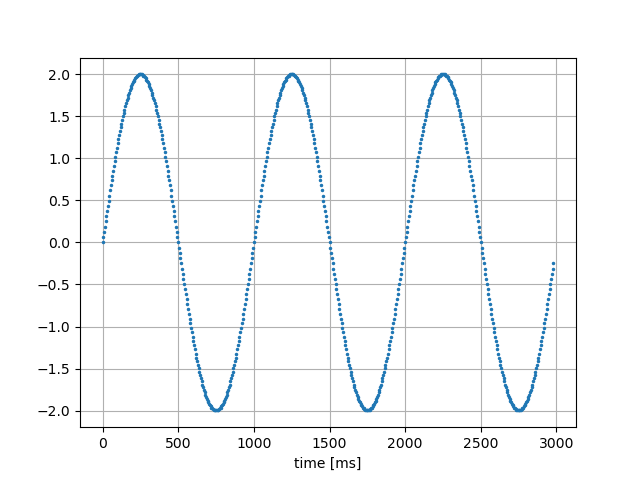
サンプリング周波数が50Hzなので、1枚目のグラフより20ms間隔のデータであることが確認できます。

この時系列データを20ms→5msにリサンプリングすることを考えます。

5msは20msの約数なので直接リサンプリングすることが可能です。しかし、今回は汎用性を考慮して、いったん20ms→1msにして、その後に1ms→5msにする方法を採用します。

なお、sin波の作成方法については、以下の記事を参考にしてください。

ディジタル信号処理｜周波数解析(FFT)をPythonで実装

アップサンプリング

        # DataFrameに格納
        self.df1 = pd.DataFrame({'ts':t, 'sig':sin})
        #print(self.df1)

        # いったん日付に変換
        self.df1['ts'] = pd.to_datetime(self.df1['ts'], unit='ms')  # デフォルトはnsなのでmsに指定
        #print(self.df1)

        # indexにセット
        self.df1 = self.df1.set_index('ts')

        # 20ms→1ms
        self.df2 = self.df1.resample('1ms').interpolate()
        #self.df2 = self.df1.resample('1ms').ffill()  # 前の値で補完

アップサンプリングはpandasのメソッドであるpandas.DataFrame.resample()を使う方法が簡単なので、まずDataFrameに格納します。

pandas.DataFrame.resample()ではDataFrameのindexを基準にリサンプリングを行うので、時間列tsをindexに設定する必要があります。

ただし、デフォルトのままだとnsオーダで認識されてしまうので、pandas.to_datetime()を使う際に、unit='ms'としてmsに指定します。

2枚目のグラフより、1msにアップサンプリングできていることが確認できます。

ダウンサンプリング

        # 20ms→1ms→5ms
        self.df3 = self.df2.asfreq('5ms')
        #self.df3 = self.df1.resample('5ms').interpolate()  # 20ms→5ms線形補間もできる

        # index解除
        self.df1.reset_index(inplace=True)
        self.df2.reset_index(inplace=True)
        self.df3.reset_index(inplace=True)

        # datetime64型→int64型｜msに戻す
        self.df1['ts'] = self.df1['ts'].astype('int64') / 10**6  # 最後の除算でns→msにする
        self.df2['ts'] = self.df2['ts'].astype('int64') / 10**6  # 最後の除算でns→msにする
        self.df3['ts'] = self.df3['ts'].astype('int64') / 10**6  # 最後の除算でns→msにする

ダウンサンプリングは、pandas.DataFrame.asfreq()を使います。

この後に元の形に戻す際には、時刻をdatetime64型からint64型にして、さらにmsにする必要があります。

3枚目のグラフより、5msにリサンプリングできていることが確認できます。

pandas.DataFrame.resample()とpandas.DataFrame.asfreq()

ここまでの説明でわかるかと思いますが、pandas.DataFrame.resample()はアップサンプリング、pandas.DataFrame.asfreq()はダウンサンプリングのメソッドとして使います。

メソッド名から見るとpandas.DataFrame.resampleはアップサンプリングもダウンサンプリングもできそうなんですが、少なくとも私が想像する使い方には対応してないようです。¹

これが私を混乱させた最大の元凶であり、記事を書くモチベーションになったところです(T_T)

考察

少し考察してみます。

3msにリサンプリングしたいとき

5msは20msの約数なので直接リサンプリングすることが可能です。しかし、今回は汎用性を考慮して、いったん20ms→1msにして、その後に1ms→5msにする方法を採用します。

と上記で述べました。そこで、ここでは3msへのリサンプリングを考えてみます。

20ms→3msへ直接リサンプリングしたときの結果は以下の通りです。

上記のグラフより、不自然にカクついた波形になっていることがわかります。

20ms→1ms→3msという流れでリサンプリングしたときの結果は以下の通りです。

計算量は増えてしまいますが、こちらの方がキレイにリサンプリングできることがわかります。

前方の値で穴埋め

サンプルプログラムでは線形補間を使って、アップサンプリングで生じる欠損値の穴埋めを行いました。

これを前方の値で穴埋めしてみます。20ms→1msffillした結果と、20ms→1msffill→5msした結果は次の通りです。

前方や後方の値で欠損値を補間する方法は、統計データに対しては一般的に使用されます。

しかし、今回のような時系列データに対しては、（少なくともこのままでは）適さないことがわかります。

エイリアシング

リサンプリングすると、一般にエイリアシングが発生してしまいます。エイリアシングとは折り返し雑音ともいいますが、本来の信号ではない偽信号が発生する現象です。

サンプルプログラムで作成した5msの時系列データを拡大すると、以下のようなギザギザした箇所が確認できます。

したがって、リサンプリングした後にこのノイズを除去（アンチエイリアシング）する必要があることに注意しましょう。

おわりに

考察も書いたので、意外とボリュームが大きくなってしまいました。

今回はしませんでしたが、リサンプリング後の波形をFFTして周波数領域で観察すると、さらに理解が深まります。
また、アップサンプリングには線形補間ではなく、ゼロで穴埋めをしてその後フィルタリング処理をし波形をなめらかにするゼロ補間という手法もあるので、余裕がある方は試してみてください。

参考になれば幸いです(^^)

参考文献

サンプルプログラムでぜひ試してみてください。↩

ari23の研究ノート

メーカ勤務エンジニアの技術ブログです