ディジタル信号処理|周波数解析とFFT(実践) - ari23の研究ノート
で作ったサンプルプログラムを使って、窓関数について少し議論したいと思います。
今回の内容は、もともと前回記事に書いていたのですが、全体のボリュームが大きくなってしまったので、切り離しました。
したがって、前回の内容が前提となりますので、ぜひ上記リンクからご覧になってください🐜
窓関数の使用について
実際に取得できる信号は両端が不連続である波形ですので、窓関数の利用は必須だと思います1。
しかし、数ある窓関数の中から何を使えばいいのかと悩みを抱えている方が多いと思います。
実は私も、そのうちの1人ですorz
以前勤めていた会社の友人で、音声認識のスペシャリストに聞いたところ、
「いいか?何も考えずにハン窓かハミング窓を使え。ん?理由だと?とにかく、どっちか使っとけ。これでこの話は終わりだ。」
と言われましたw
説明しても理解できないだろうと思われた可能性もありますが、
一方でどの文献を読んでも、窓関数にきちんと言及しているものは見当たりません。
「よく使われるのはHann窓やHaminng窓です」程度で、使い分けについて明言を避けているような気がします2。
今のところの私の考えは、
- とりあえず、みんなが使っているハン窓やハミング窓を使って、自分の結果と比較できるようにする
- もし、一般には使わない窓関数で良い分析結果が得られる場合は、それを論文なり文書なりに必ず明記する
です。
ただ、せっかくなのでHann窓とHamming窓の特徴くらいは把握しておこうと思います。
Hann窓とHamming窓の一般的知識
大体以下のような特徴があります。
| 窓関数 | 特徴 |
|---|---|
| Hann窓 | ・両端がゼロで連続 ・振幅の小さい周波数も検出しやすい ・少し波形がなまる |
| Hamming窓 | ・両端がゼロでなく不連続 ・Hann窓の改良版 ・周波数分解能が高い |
Hann窓とHamming窓の比較
では、実際にHann窓とHamming窓を使ったFFTの結果を比較します。
ソースコードはこちらを参考に、適宜Hann窓とHamming窓を畳み込むところのコメントアウトをつけたり、外したりしてください。
以下にHann窓とHamming窓の結果を記載します。
Hann窓

Hann窓でFFTした例 Hamming窓
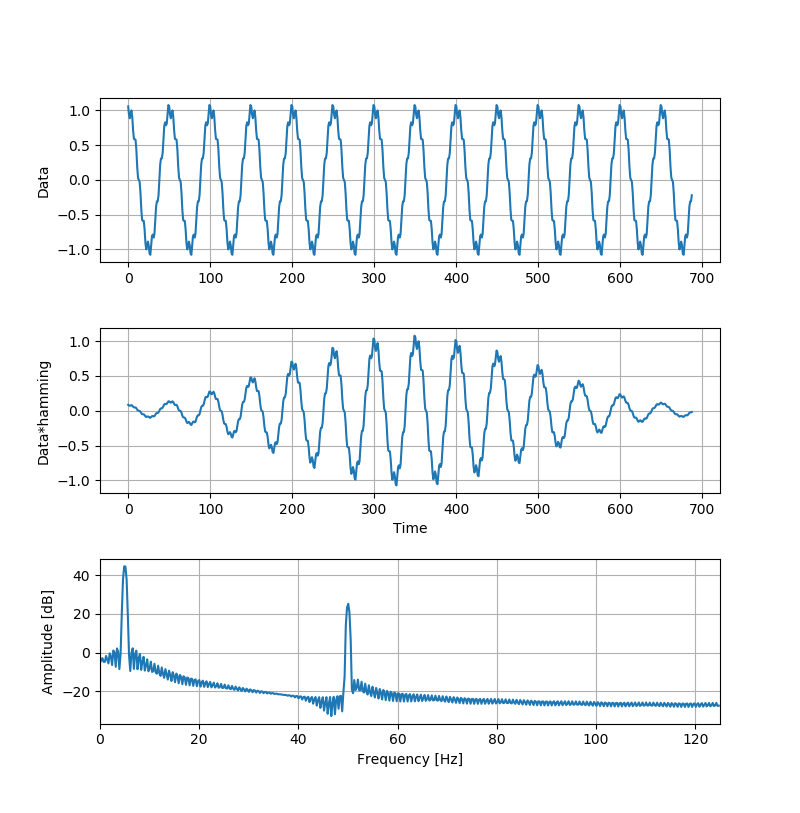
Hamming窓でFFTした例
まず、両者の畳み込みの結果(真ん中のグラフ)を見ると、たしかに両端が不連続になっていることがわかります。
そして、両者のFFTの結果(一番下)を見ると、Hamming窓のほうがピークの立ちがはっきりしています。
一方で5Hzと50Hz以外の周波数帯において、縦軸のレンジに惑わされないよう注意深く見ると、Hann窓のほうがHamming窓より値が小さく出ているため、振幅の小さい周波数の信号でもよく検出できると言えそうです。
おわりに
今回はHann窓とHamming窓を使ったFFTの結果を比較し、それぞれの特徴を確認しました。
意外とこういった記事は少ないので、貴重な情報なのではと思っています。
参考になれば幸いです(^^)