データ同化｜カルマンフィルタと斜方投射への適用例

この記事では、以下の記事の続きとして、カルマンフィルタを斜方投射（放物線運動）に適用した例を書きます🐜

データ同化｜カルマンフィルタと尤度 - ari23の研究ノート

今回はカルマンフィルタの立式までとし、プログラムの実装とパラメタの設定は次回とします。

斜方投射
- 空気抵抗あり
- 空気抵抗なし
状態空間モデル
おわりに
参考文献

斜方投射

「斜方投射」というとちょっと難しい印象ですが、だたのボールを斜めに投げる放物線運動です。高校物理の範囲ですが、少し難しくするために空気抵抗を考慮します。

したがってここでは、真のモデル ${f_t}^{perfect}$ を空気抵抗ありのモデル式、シミュレーションモデル $f_t$ を空気抵抗なしのモデル式とし、カルマンフィルタを使って真値を予測することを目的とします。

空気抵抗あり

質量 $m$ のボールを角度 $\theta$ で投げたときのボールのxy座標を式で求める。初速は $v_0$ で、初期位置は $(0, 0)$ 、空気抵抗は速度に比例し $r$ とする。なお、ボールの大きさは考えない。

項目	内容
質量	$m$ [kg]
初速	$v_0$ [m/s]
初期座標	$(0, 0)$ [m]
投射角度	$\theta$ [rad]
空気抵抗	$r$ [kg/s]
重力加速度	$g$ [m/s²]

座標系は次の通り。

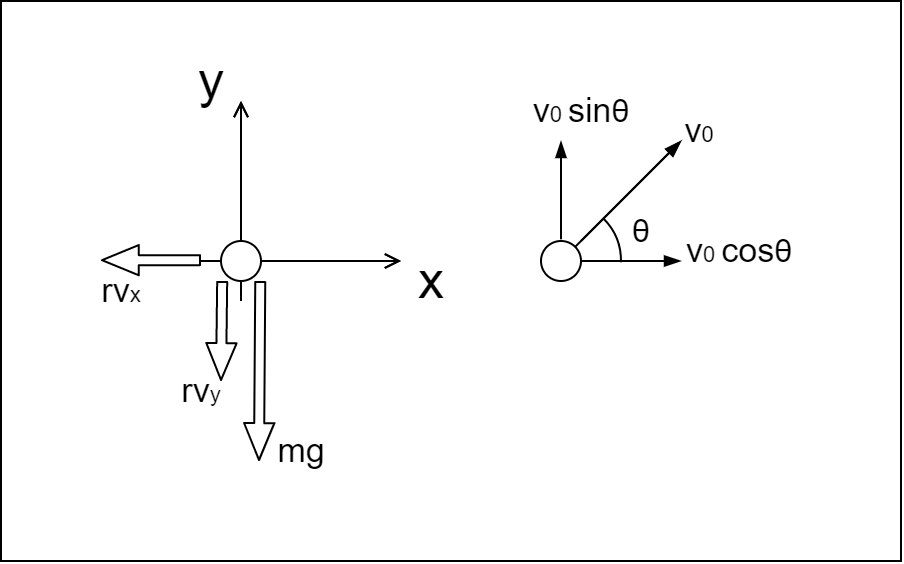
x軸とy軸の運動方程式は以下のように書ける。

$\displaystyle \begin{align} m a_x &= - r v_x \\ m a_y &= - m g - r v_y \end{align}$

両辺に $\times \frac{1}{m}$ する。

$\displaystyle \begin{align} a_x &= - \frac{r}{m} v_x \\ a_y &= - g - \frac{r}{m} v_y \end{align}$

上式より、速度は以下のように書ける。

$\displaystyle \begin{align} v_x &= v_0 \cos\theta \ \exp \biggl( -\frac{r}{m} t \biggr) \\ v_y &= (v_0 \sin\theta + gt) \ \exp \biggl( -\frac{r}{m} t \biggr) - \frac{m}{r} g \end{align}$

よって、x座標とy座標は以下となる。

$\displaystyle \begin{align} x &= \frac{m v_0}{r} \biggl( 1 - \exp \Bigl( -\frac{r}{m} t \Bigr) \biggr) \cos\theta \\ y &= \frac{m}{r} \biggl\{ \biggl(v_0 \sin\theta + \frac{m}{r} g \biggr) \biggl( 1 - \exp \Bigl( -\frac{r}{m} t \Bigr) \biggr) - gt \biggr\} \end{align}$

空気抵抗なし

同様に、空気抵抗がない場合を考える。ただし、こちらは差分方程式で表す。

時刻の刻み幅を $\Delta t$ としたとき、時刻 $t$ のx座標の位置 $x_t$ 、速度 $\dot{x}_t$ 、加速度 $\ddot{x}_t$ は以下のように書ける。

$\displaystyle \begin{align} x_t &= x_{t-1} + \Delta t \ \dot{x}_{t-1} \\ \dot{x}_t &= \dot{x}_{t-1} \\ \ddot{x}_t &= \ddot{x}_{t-1} \end{align}$

$\dot{x}$ は $x$ の1回微分、 $\ddot{x}$ は $x$ の2回微分を示す。

同様にy座標は以下のように書ける。

$\displaystyle \begin{align} y_t &= y_{t-1} + \Delta t \ \dot{y}_{t-1} + \frac{(\Delta t)^2}{2} \ddot{y}_{t-1} \\ \dot{y}_t &= \dot{y}_{t-1} + \Delta t \ \ddot{y}_{t-1} \\ \ddot{y}_t &= \ddot{y}_{t-1} \end{align}$

なお、参考として、時刻 $t$ で表すときのxy座標を以下に示す。

$\displaystyle \begin{align} x_t &= v_0 \cos\theta \ t \\ y_t &= v_0 \sin\theta \ t - \frac{1}{2} g t^2 \end{align}$

状態空間モデル

今度は、空気抵抗なしのシミレーションモデルを使って、状態空間モデルを立ててみます。

線形・ガウス状態空間モデル

$\displaystyle \begin{align} \boldsymbol{x}_t &= F_t \boldsymbol{x}_{t-1} + G_t \boldsymbol{v}_t \qquad \boldsymbol{v}_t \sim N(\boldsymbol{0}, Q_t)\\ \boldsymbol{y}_t &= H_t \boldsymbol{x}_t + \boldsymbol{w}_t \qquad \quad \ \boldsymbol{w}_t \sim N(\boldsymbol{0}, R_t) \end{align}$

システムモデル

状態変数をx軸の位置、速度、加速度と、y軸の位置、速度、加速度を含んだベクトルとする。つまり、 $\boldsymbol{x}_t=[x_t, \dot{x}_t, \ddot{x}_t, y_t, \dot{y}_t, \ddot{y}_t]^{\prime}$ とおく。
簡単のためシステムノイズを省略すると、以下のように書ける。

$\displaystyle \begin{align} \boldsymbol{x}_t &= F_t \boldsymbol{x}_{t-1} \\ \Leftrightarrow \left[ \begin{array}{c} x_t \\ \dot{x}_t \\ \ddot{x}_t \\ y_t \\ \dot{y}_t \\ \ddot{y}_t \\ \end{array} \right] &= \begin{bmatrix} 1 & \Delta t & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & \Delta t & \frac{(\Delta t)^2}{2} \\ 0 & 0 & 0 & 0 & 1 & \Delta t \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} \left[ \begin{array}{c} x_{t-1} \\ \dot{x}_{t-1} \\ \ddot{x}_{t-1} \\ y_{t-1} \\ \dot{y}_{t-1} \\ \ddot{y}_{t-1} \\ \end{array} \right] \end{align}$

観測モデル

今回の系では、x軸の位置とy軸の位置が観測できるとする。つまり、 $\boldsymbol{y}_t=[x_t, y_t]^{\prime}$ とおく。
簡単のため観測ノイズを省略すると、以下のように書ける。

$\displaystyle \begin{align} \boldsymbol{y}_t &= H_t \boldsymbol{x}_{t} \\ \Leftrightarrow \left[ \begin{array}{c} x_t \\ y_t \\ \end{array} \right] &= \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ \end{bmatrix} \left[ \begin{array}{c} x_t \\ \dot{x}_t \\ \ddot{x}_t \\ y_t \\ \dot{y}_t \\ \ddot{y}_t \\ \end{array} \right] \end{align}$

組み立てのポイント

状態空間モデルを立てるときに一番重要なことは、状態変数 $\boldsymbol{x}_t$ の要素です。今回はすべての同じ時刻 $t$ でしたが、たとえばシミレーションモデルがARモデル（自己回帰モデル）であれば、 $t-1$ など他の時刻の要素が入ってきます。

おわりに

斜方投射を題材に、状態空間モデルを立ててみました。かなり丁寧に書いたので、比較的わかりやすいかと思います。

参考になれば幸いです(^^)

なお、Pythonでの実装例は以下になります。こちらも、ぜひご覧ください。

データ同化｜斜方投射のカルマンフィルタをPythonで実装 - ari23の研究ノート

参考文献

参考文献は以下の通りです。

データ同化入門 (予測と発見の科学)
データ同化分野で私にとってのバイブルです。決して簡単ではないですが、数学的議論がかなりきちんとなされています。データ同化に取り組むときは、まずこれを読んでいます。
カルマンフィルタの基礎
工学の視点からカルマンフィルタが丁寧に説明されています。カルマンフィルタならこれがおすすめです。
時系列解析の方法 (統計科学選書)
カルマンフィルタはもちろん、タイトル通り時系列解析の手法が解説されています。比較的読みやすいです。

リンク